Die allermeisten Programme haben mit derselben grössten Herausforderung zu kämpfen: dem Benutzer. Der Fall, dass der Benutzer genau diejenigen Eingaben macht, welche vorgesehen sind, ist eigentlich eher ein Spezialfall, und die Qualität eines Programms ist häufig dadurch bestimmt, wie viele der Falscheingaben es abdecken kann.
Eine nicht selten vorkommende Sorte Falscheingabe sind Tippfehler. Das Konzept der Levenshtein-Distanz bietet eine mögliche Lösung, um auch Eingaben mit einer kleinen Menge an Fehlern zu identifizieren.
Levenshtein-Distanz
Benannt nach Vladimir Levenshtein, welcher dieses Konzept 1965 erarbeitet hat, gibt die Levenshtein-Distanz an, wie viele Änderungen an einer Zeichenkette vorgenommen werden müssen, damit sie mit einer anderen übereinstimmt. Um von der einen zur anderen Zeichenkette zu kommen, können folgende Änderungen vorgenommen werden:
- Insert: Ein beliebiges Zeichen an beliebiger Stelle einfügen
- Delete: Ein Zeichen an beliebiger Stelle löschen
- Substitute: Ein Zeichen an einer beliebigen Stelle durch ein anderes ersetzen.
Jede dieser Aktionen ist gleichwertig und zählt "+1". Die Summe, die man am Ende erhält ist die Levenshtein-Distanz, sofern es der kürzestmögliche Weg war.
Beispiel: Die Levenshtein-Distanz zwischen "Abreitsjournl" und "Arbeitsjournal" ist 3, denn es werden mindestens drei Schritte benötigt, um von "Abreitsjournl" zu "Arbeitsjournal" zu kommen:
- Ersetze das Zeichen "b" durch "r". ("Arreitsjournl")
- Ersetze das zweite "r" durch "b". ("Arbeitsjournl")
- Füge ein "a" ein. ("Arbeitsjournal")
Wenn jetzt zum Beispiel nach allen Dokumenten gesucht wird, welche mit dem Wort "Arbeitsjournal" beginnen, können auch Dokumente berücksichtigt werden, welche wenig genug Schreibfehler haben, dass man sich immer noch sicher genug sein kann, dass "Arbeitsjournal" gemeint war. Und zwar, indem man prüft, ob die Levenshtein-Distanz zwischen Dokumentenname und "Arbeitsjournal" kleiner als die höchste zulässige Levenshtein-Distanz ist.
Wagner-Fischer-Algorithmus - Idee
Der Wagner-Fischer-Algorithmus (welcher unter anderem von den namensgebenden Personen erfunden wurde) berechnet die Levenshtein-Distanz zwischen zwei Zeichenketten programmatisch. Das Prinzip dabei ist, dass iterativ eine Matrix aufgebaut wird, wobei in jeder Zelle die Levenshtein-Distanz zwischen Teilen der betrachteten Zeichenketten zu stehen kommt. Denn die Problemstellung wie man z.B. von "Abreit" nach "Arbeit" kommt ist ein Teilproblem von wie man von "Abreitsjournl" nach "Arbeitsjournal" kommt.
Die Levenshtein-Distanz des Gesamt-Problems steht dann in der Zelle rechts unten der Matrix.
Die vollständige Matrix dieses Beispiels sieht so aus:

Wie erwähnt sind bei der Levenshtein-Distanz drei Aktionen zulässig: Ein Zeichen einfügen, löschen oder ersetzen. Diese Aktionen können verwendet werden, um durch diese Matrix zu "navigieren". Dabei beginnt man immer im Feld ganz oben links (dieses Feld enthält die Levenshtein-Distanz um von einem leeren String zu einem leeren String zu kommen, und ist somit immer 0). Man kann nun in drei Richtungen "gehen":
- nach unten = ein Zeichen löschen
- nach rechts = ein Zeichen einfügen
- diagonal nach unten rechts = ein Zeichen ersetzen
Wenn ein Buchstabe mit demselben Buchstaben ersetzt wird (ersetze "a" mit "a") zählt dies +0 zur Levenshtein-Distanz.
Als Beispiel dazu nur mal das Unterproblem 'wie kommt man von "ab" nach "ar"?'. Man kann dieses Problem auf verschiedene Arten lösen, aber nur eine führt zur richtigen Levenshtein-Distanz:

- Ersetze "a" mit "a": +0
- Ersetze "b" mit "r": +1
Änderungen: 1
Diese Zahl stimmt mit der Zahl unten rechts überein, also war dies der richtige Weg und die Levenshtein-Distanz ist 1.

- Ersetze "a" mit "a": +0
- Füge ein "r" ein: +1
- Lösche "b": +1
Änderungen: 2.
Diese Zahl stimmt nicht mit der Zahl unten rechts überein. Also war dies nicht der schnellste Weg.

- Lösche "a": +1
- Lösche "b": +1
- Füge "a" hinzu: +1
- Füge "r" hinzu: +1
Änderungen: 4
Hier noch der Weg für "Abreitsjournl" nach "Arbeitsjournal". Die zählenden Änderungen finden immer dort statt, wo sich die Levenshtein-Distanz erhöht.

Wagner-Fischer-Algorithmus - Realisierung
Es braucht nicht sehr viel Code um diesen Algorithmus zu realisieren. Eine mögliche Umsetzung in C# sieht wie folgt aus:
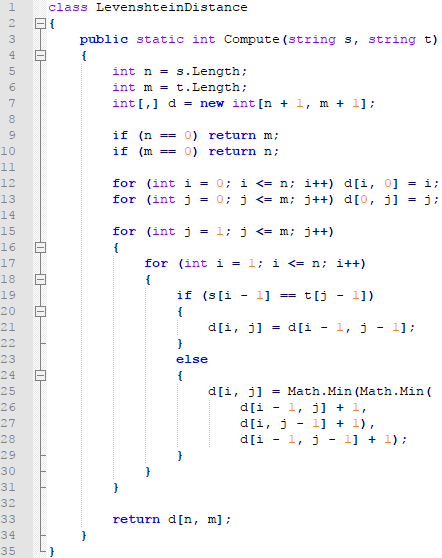
Die Variablen, welche hier zum Zuge kommen, sind:
- s und t: Die zu vergleichenden Zeichenketten.
- n und m: Die Längen der Zeichenketten.
- d: Zweidimensionales Array, welches der obigen Matrix entspricht. Speziell anzumerken ist, dass die Dimensionen um 1 grösser sind als die Längen der Strings.
In den Zeilen 9 und 10 werden die Spezialfälle behandelt, dass einer der beiden Strings leer ist. In diesen Fällen kann schnell gesagt werden, dass jedes Zeichen anders ist und somit die Anzahl Änderungen der Anzahl Zeichen der ausgehenden bzw. zu erreichenden Zeichenkette entspricht.
In den Zeilen 12 und 13 wird die erste Spalte und Zeile mit aufsteigenden Zahlen gefüllt (auch diese Zahlen sind Levenshtein-Distanzen!).
In den Zeilen 15 und 17 wird über alle Zellen der Matrix iteriert. Da die erste Spalte und Zeile schon befüllt wurde, wird mit dem Index 1 statt 0 begonnen. Da die Matrix-Dimensionen um 1 grösser sind als die Längen der Strings (n und m) wird mit "kleiner-gleich" statt "strikt-kleiner" gearbeitet.
In den Zeilen 19 bis 29 werden die Zellen befüllt:
Es werden erst einmal zwei Fälle unterschieden, je nachdem, ob diejenigen Zeichen der Strings, welche über der aktuellen Matrix-Zelle stehen identisch sind. (i und j sind 1-indiziert, die Zeichenposition ist aber 0-indiziert, deshalb wird s[i-1] und t[j-1] und nicht s[i] und t[j] verglichen).
Ist dies der Fall wird die Levenshtein-Distanz aus der Zelle diagonal oben links übernommen. Dies entspricht der Aktion 'ersetze "a" mit "a"', welche nichts "kostet", und dies ist garantiert der schnellste Weg, um die aktuelle Position zu erreichen.
Andernfalls kostet es "+1" um zu der aktuellen Position zu kommen. Dies kann durch Einfügen, Löschen oder Ersetzen geschehen. Um herauszufinden, welche dieser Aktionen die beste ist, muss geschaut werden, wie teuer es ist, an die Ausgangsposition der jeweiligen Aktionen zu kommen. Man nehme dieses Beispiel nochmals:

Noch einmal: Zuerst wird geprüft, ob die Zeichen an den entsprechenden Positionen identisch sind. "b" ist nicht gleich "r". Wir haben also drei Möglichkeiten:
- Ausgehend von "a" ein "r" einfügen
- Ausgehend von "abr" das "b" löschen
- Ausgehend von "ab" das "b" durch ein "r" ersetzen.
Alle drei Aktionen kosten "+1". Der Unterschied ist aber, dass es bereits "1" kostet, um zu "a" oder "abr" zu gelangen, hingegen kostet es "0" um zu "ab" zu gelangen. Somit ist es am günstigsten, von "ab" auszugehen. Dann kostet es "0 +1", also "1".
Programmatisch wird dazu die kleinste aus den drei Zahlen, die links, oben und links oben der gesuchten Zahlen steht gefunden und um 1 erhöht.
Quellen:
- https://en.wikipedia.org/wiki/Levenshtein_distance
- https://en.wikipedia.org/wiki/Wagner%E2%80%93Fischer_algorithm
- https://www.kleemans.ch/levenshtein-distance (insbesondere zur Generierung der Matrizen)
